對于(At)一(One)些分布式存儲的(Of)一(One)級市場來說，存在(Exist)一(One)種出(Out)錢和(And)出(Out)力的(Of)博弈。

比如Filecoin，有人(People)手裏用(Use)來質押的(Of)代币較多，但是(Yes)設備硬件條件不(No)足；有的(Of)人(People)則恰好相反，技術能力較強，在(Exist)硬件設備方面投入較多，卻需要(Want)通過貸款獲得代币進行抵押。

對于(At)資本和(And)硬件的(Of)雙重要(Want)求使得分布式存儲的(Of)門檻升高，系統有中心化的(Of)風險。

由于(At)質押FIL和(And)硬件投入的(Of)成本對于(At)不(No)同的(Of)存儲提供商來說成本都不(No)一(One)樣，如果可以(By)将這(This)兩種人(People)手中的(Of)資源進行整合，并以(By)一(One)種合理的(Of)方式“拼單”，提高整體收益并公平地分配收益，筆者想就可以(By)降低存儲提供商的(Of)門檻，讓更多的(Of)人(People)參與進來。

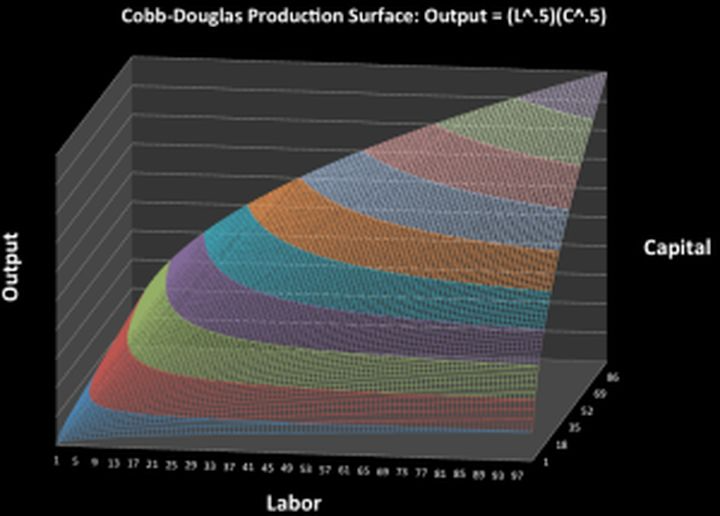
柯布一(One)道格拉斯生産函數

“出(Out)錢”和(And)“出(Out)技術”（出(Out)力）可以(By)抽象成經濟模型中的(Of)資本投入和(And)勞動力投入。而在(Exist)規模報酬不(No)變的(Of)生産技術下，勞動力回報和(And)資本回報會分割總産出(Out)。

從長期來看，在(Exist)一(One)些大(Big)的(Of)經濟體中，資本回報與勞動力回報占比的(Of)基本保持穩定。

20世紀初，美國(Country)有位名叫道格拉斯( Paul Douglas)的(Of)參議員同時(Hour)也是(Yes)一(One)位經濟學家，他(He)研究了(Got it)1899-1922年美國(Country)制造業的(Of)數據，發現資本和(And)勞動力在(Exist)産出(Out)中的(Of)份額保持不(No)變。于(At)是(Yes)，他(He)找到他(He)大(Big)學的(Of)數學老師柯布( Charles Cobb)，詢問什麽樣的(Of)生産函數能産生這(This)樣的(Of)特性。在(Exist)柯布構造出(Out)了(Got it)這(This)樣的(Of)生産函數後，他(He)們于(At)1928年發表了(Got it)一(One)篇文章，提出(Out)了(Got it)著名的(Of)柯布一(One)道格拉斯生産函數(Cobb- Douglas production function)，是(Yes)微觀經濟學上(Superior)用(Use)來描述生産函數的(Of)常用(Use)函數之一(One)。

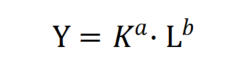
其中，a叫做資本權重，1-a叫做“勞動力權重”。 

如果把 Cobb-Douglas 方程放到更廣泛的(Of)場景下，它是(Yes)通過一(One)種加權幾何的(Of)方式，來在(Exist)兩者或多方貢獻者之間分配一(One)筆收入的(Of)函數。

目前，就筆者有限的(Of)知識，區塊鏈世界中應用(Use)到Cobb-Douglas方程來分配獎勵的(Of)項目較少，隻有DeFi中的(Of) 0x協議 和(And)鏈上(Superior)數據檢索 The Graph 在(Exist)其經濟模型中有涉及。

0x協議

0x協議是(Yes)一(One)種去中心化交易協議，其開源的(Of)基礎架構使開發人(People)員和(And)企業能夠構建自己的(Of)交易所來交易所有ERC-20和(And)ERC-721資産。

由于(At)流動性能夠促進整個(Indivual)經濟系統的(Of)穩定（尤其是(Yes)交易深度），使得經濟系統具有一(One)定的(Of)彈性，在(Exist)一(One)定程度上(Superior)抵抗來自外界的(Of)不(No)良沖擊。

于(At)是(Yes)就額外從每筆交易中收集的(Of)“Protocol Fee”的(Of)池子中分給交易中的(Of)發起方（Maker），也就是(Yes)給流動性的(Of)貢獻者提供了(Got it)一(One)筆獎勵。

那麽，在(Exist)一(One)段時(Hour)間内如何在(Exist)所有的(Of)Maker之間分配這(This)筆額外獎勵呢？

其中有兩個(Indivual)重要(Want)因素，一(One)個(Indivual)是(Yes)代表Maker質押SRX（0x原生代币）占整體質押量的(Of)比例τ ，和(And)該Maker對Protocol Fee貢獻占整個(Indivual)獎勵池的(Of)比例z 。

它們之間通過α 和(And)1-α 在(Exist)指數位置的(Of)加權，得到該Maker在(Exist)獎勵池中的(Of)份額S。

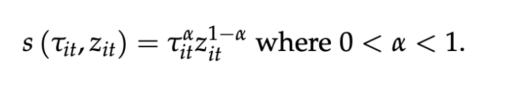
我們可以(By)把公式中的(Of) τ 理解爲(For)Maker質押SRX的(Of)成本（如币價的(Of)波動或損失的(Of)利息），或者是(Yes)貸款的(Of)利息成本，z 理解爲(For)提供交易的(Of)成本，則 α 和(And) 1-α 則分别是(Yes)給定的(Of)兩種成本的(Of)比重。

 在(Exist)0x協議中，不(No)同Maker手中SRX和(And)提供流動性的(Of)代币的(Of)成本各不(No)相同。

如果Maker認爲(For)質押某個(Indivual)數量的(Of)SRX的(Of)成本（或風險）大(Big)于(At)提供流動性的(Of)成本，此時(Hour)不(No)如将多餘的(Of)SRX借出(Out)去。相反也是(Yes)如此。

The Graph

而在(Exist)The Graph中，則是(Yes)爲(For)了(Got it)鼓勵索引者（Indexer）而返還一(One)部分的(Of)Protocol Fee作(Do)爲(For)獎勵。

在(Exist)考慮索引者給子圖的(Of)質押量ω占該子圖的(Of)比例和(And)給返還池貢獻的(Of)查詢費Θ的(Of)占比這(This)兩個(Indivual)因素後，給出(Out)某個(Indivual)索引者在(Exist)這(This)批獎勵池中的(Of)占比：

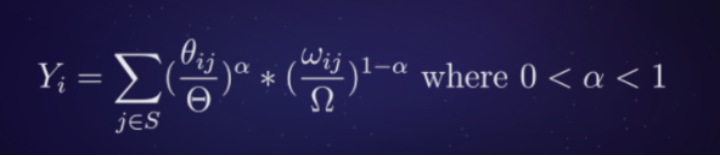
同樣，索引者需要(Want)平衡質押The Graph代币GRT的(Of)成本和(And)索引服務的(Of)運營成本，以(By)達到從獎勵池中分得更大(Big)的(Of)份額。

抛出(Out)問題

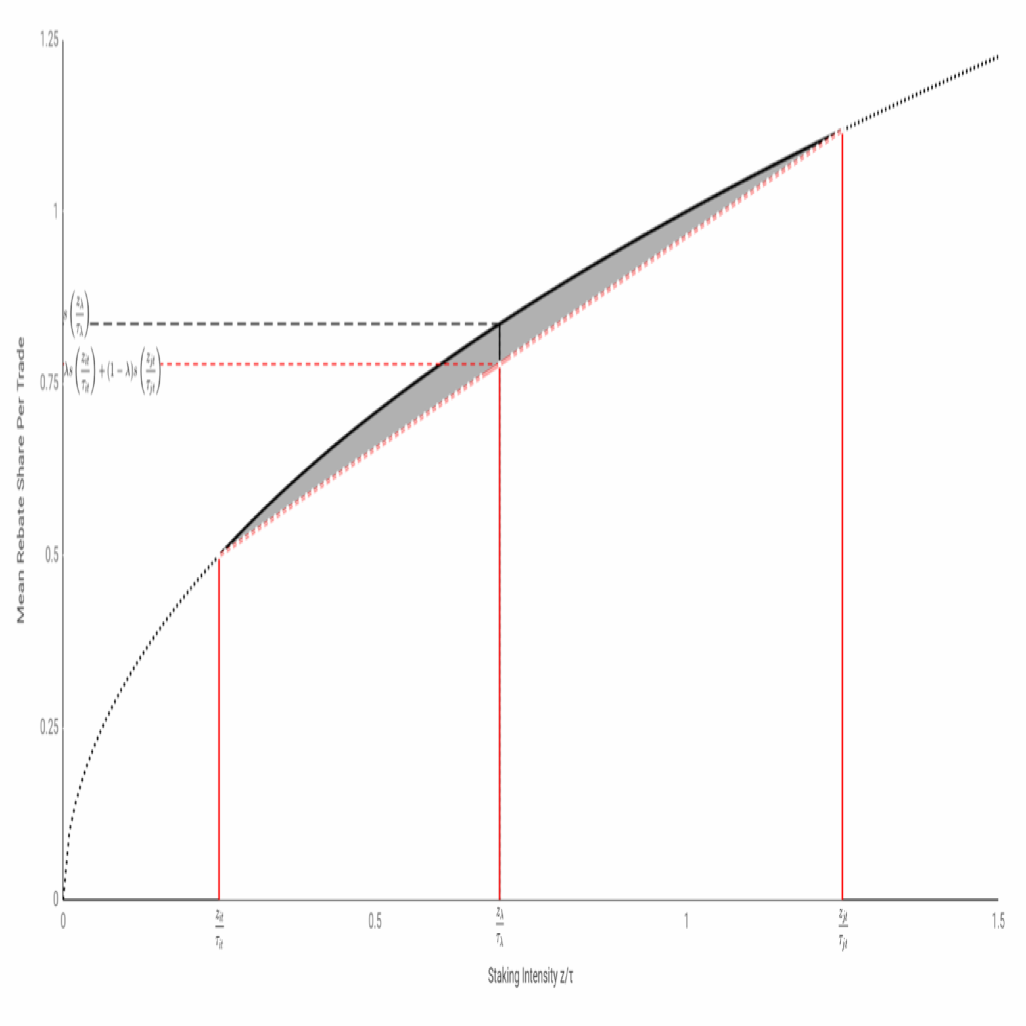
由于(At)質押FIL和(And)硬件投入的(Of)成本對于(At)不(No)同的(Of)存儲提供商來說成本都不(No)一(One)樣，如果想實現1 + 1 > 2的(Of)效果，提高整體存儲收益，那麽“出(Out)錢”和(And)“出(Out)力”二者的(Of)結合需要(Want)一(One)種合理的(Of)資源配置和(And)公平的(Of)收益分配。

柯布-道格拉斯函數有一(One)個(Indivual)獨特的(Of)性質，即無論外部市場條件如何變化，收入在(Exist)“出(Out)錢”和(And)“出(Out)力”者之間的(Of)分配始終保持不(No)變。

這(This)其實是(Yes)一(One)個(Indivual)在(Exist)規則下動态平衡的(Of)過程，如果提供的(Of)質押過多，則收益會低于(At)将這(This)部分多餘的(Of)質押借出(Out)去的(Of)情況。